Teoria do caos, para a física e a matemática, é a teoria que explica o funcionamento de sistemas complexos e dinâmicos. Em sistemas dinâmicos complexos, determinados resultados podem ser "instáveis" no que diz respeito à evolução temporal como função de seus parâmetros e variáveis. Isso significa que certos resultados determinados são causados pela ação e a iteração de elementos de forma praticamente aleatória. Para entender o que isso significa, basta pegar um exemplo na natureza, onde esses sistemas são comuns. A formação de uma nuvem no céu, por exemplo, pode ser desencadeada e se desenvolver com base em centenas de fatores que podem ser o calor, o frio, a evaporação da água, os ventos, o clima, condições do Sol, os eventos sobre a superfície e inúmeros outros.
Além disso, mesmo que o número de fatores influenciando um determinado resultado seja pequeno, ainda assim a ocorrência do resultado esperado pode ser instável, desde que o sistema seja não-linear.
A conseqüência desta instabilidade dos resultados é que mesmo sistemas determinísticos (os quais tem resultados determinados por leis de evolução bem definidas) apresentem uma grande sensibilidade a perturbações (ruído) e erros, o que leva a resultados que são, na prática, imprevisíveis ou aleatórios, ocorrendo ao acaso. Mesmo em sistemas nos quais não há ruído, erros microscópicos na determinação do estado inicial e atual do sistema podem ser amplificados pela não-linearidade ou pelo grande número de interações entre os componentes, levando ao resultado aleatório. É o que se chama de "Caos Determinístico"
Na verdade, embora a descrição da mecânica clássica e relativística seja determinística, a complexidade da maioria dos sistemas leva a uma abordagem na qual a maioria dos graus de liberdade microscópicos é tratada como ruído (variáveis estocásticas, ou seja, que apresentam valores verdadeiramente aleatórios) e apenas algumas variáveis são analisadas com uma lei de comportamento determinada, mais simples, sujeita à ação deste ruído. Este método foi utilizado por Einstein e Langevin no início do século XX para compreender o Movimento Browniano.
Pois, é exatamente isso que os matemáticos querem prever: o que as pessoas pensam que é acaso mas, na realidade, é um fenômeno que pode ser representado por equações. Alguns pesquisadores já conseguiram chegar a algumas equações capazes de simular o resultado de sistemas como esses, ainda assim, a maior parte desses cálculos prevê um mínimo de constância dentro do sistema, o que normalmente não ocorre na natureza.
Os cálculos envolvendo a Teoria do Caos são utilizados para descrever e entender fenômenos meteorológicos, crescimento de populações, variações no mercado financeiro e movimentos de placas tectônicas, entre outros. Uma das mais conhecidas bases da teoria é o chamado "efeito borboleta", teorizado pelo matemático Edward Lorenz, em 1963.
-----------xxx--------------
Efeito borboleta é um termo que se refere à dependência sensível às condições iniciais dentro da teoria do caos. Este efeito foi analisado pela primeira vez em 1963 por Edward Lorenz. Segundo a cultura popular, a teoria apresentada, o bater de asas de uma simples borboleta poderia influenciar o curso natural das coisas e, assim, talvez provocar um tufão do outro lado do mundo. Porém isso se mostra apenas como uma interpretação alegórica do fato. O que acontece é que quando movimentos caóticos são analisados através de gráficos, sua representação passa de aleatória para padronizada depois de uma série de marcações onde o gráfico depois de analisado passa a ter o formato de borboleta.
Teoria do caos
O efeito borboleta faz parte da teoria do caos, a qual encontra aplicações em qualquer área das ciências: exatas (engenharia, física, etc), médicas (medicina, veterinária, etc), biológicas (biologia, zoologia,botânica, etc) ou humanas (psicologia, sociologia, etc), na arte ou religião, entre outras aplicações, seja em áreas convencionais e não convencionais. Assim, o Efeito Borboleta encontra também espaço em qualquer sistema natural, ou seja, em qualquer sistema que seja dinâmico, complexo e adaptativo. Existe um filme com o nome "The Butterfly Effect" (Efeito Borboleta) fazendo referência a esta teoria.
Dinamismo do efeito borboleta
Esse tipo de efeito quando restrito a uma ou duas variáveis, fixando-se as demais, tende a ser simples e aí, somente nesta situação não natural ou limítrofe, é que as leis da ciência clássica podem demonstrar a previsibilidade de um sistema fechado. Neste caso aumenta a rigidez sistêmica e o Efeito Borboleta pode ser mapeado de forma bastante simples. Alguns estudiosos afirmam que deixa de existir, porém, é conhecido que a resultante de determinado cálculo quando passa a ser dado numérico de outro (e assim por diante), influi em seu resultado, portanto, atua o Efeito Borboleta. Isto foi descoberto (quase por acaso) por Edward Lorenz quando estava trabalhando com previsões meteorológicas no MIT e verificou a influência ocasionada em sistemas dinâmicos quando são feitas alterações muito pequenas nos dados iniciais inseridos em computadores numéricos programados para fazerem cálculos em série.
Descrição de ocorrência do efeito borboleta
Em 19 de fevereiro de 1998, computadores do sistema de previsão de tempestades tropicais dos Estados Unidos diagnosticaram a formação de uma tempestade tropical sobre Louisiana em três dias. Sobre o Oceano Pacífico um meteorologista daquela agência descobriu que havia uma pequena diferença nas medições executadas, e que estas poderiam prever uma pequena diferença no deslocamento das massas de ar. A diferença foi detectada através de uma movimentação do ar em maior velocidade na região do Alasca. Em função das diferenças, houve uma realimentação de dados nos computadores, estes refazendo os cálculos previram que a formação da tempestade tropical em Lousiana não ocorreria, mas haveria sim a formação de um tornado de proporções gigantescas em Orlando, na Flórida, o que realmente ocorreu em 22 de fevereiro de 1998.
Somatória do erro e incerteza dos sistemas rígidos
Na ciência clássica, em geral se transformam os sistemas abertos, ou seja, os sistemas dinâmicos, complexos e adaptativos, em sistemas fechados para poder aplicar as leis conhecidas que privilegiam as linearidades em detrimento das não-linearidades. Isto ocorre para facilitar e simplificar a análise de dados. Mas, ao se tomar uma decisão mínima, considerada muitas vezes insignificante, tomada com plena espontaneidade, nos sistemas dinâmicos abertos, poderemos gerar uma transformação inesperada num futuro incerto.
Por isto, neste tipo de sistema, quando restrito a uma ou duas variáveis fixando-se as demais, e somente nessa situação chamada limítrofe, o sistema se torna fechado, e o Efeito Borboleta aparentemente não atua, causando assim a impressão de um sistema estático.
Definição matemática
Um sistema dinâmico evoluindo a partir de 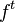 indica uma dependência estreita entre as condições finais em relação às iniciais. Se for arbitrariamente separado um ponto a partir do aumento de t, sendo um ponto qualquer M aquele que indica o estado de
indica uma dependência estreita entre as condições finais em relação às iniciais. Se for arbitrariamente separado um ponto a partir do aumento de t, sendo um ponto qualquer M aquele que indica o estado de 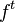 , este mostra uma sensível dependência das circunstâncias finais a partir das iniciais.
, este mostra uma sensível dependência das circunstâncias finais a partir das iniciais.
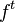 indica uma dependência estreita entre as condições finais em relação às iniciais. Se for arbitrariamente separado um ponto a partir do aumento de t, sendo um ponto qualquer M aquele que indica o estado de
indica uma dependência estreita entre as condições finais em relação às iniciais. Se for arbitrariamente separado um ponto a partir do aumento de t, sendo um ponto qualquer M aquele que indica o estado de 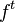 , este mostra uma sensível dependência das circunstâncias finais a partir das iniciais.
, este mostra uma sensível dependência das circunstâncias finais a partir das iniciais.
Portanto, havendo assim no início d>0 para cada ponto x em M, onde na vizinhança de N que contém x exista um ponto y e um tempo τ temos : 

---------------------------xxxx------------------------------------------
O princípio da incerteza de Heisenberg consiste num enunciado da mecânica quântica, formulado inicialmente em 1927 por Werner Heisenberg, impondo restrições à precisão com que se podem efetuar medidas simultâneas de uma classe de pares de observáveis.
Pode-se exprimir o princípio da incerteza nos seguintes termos:
O produto da incerteza associada ao valor de uma coordenada xi e a incerteza associada ao seu correspondente momento linear pi não pode ser inferior, em grandeza, à constante de Planck normalizada.[1]
Em termos matemáticos, exprime-se assim:

A explicação disso é fácil de se entender, e fala mesmo em favor da intuição, embora o raciocínio clássico e os aspectos formais da análise matemática tenham levado os cientistas a pensarem diferentemente por muito tempo
Quando se quer encontrar a posição de um elétron, por exemplo, é necessário fazê-lo interagir com algum instrumento de medida, direta ou indiretamente. Por exemplo, faz-se incidir sobre ele algum tipo de radiação. Tanto faz aqui que se considere a radiação do modo clássico - constituída por ondas eletromagnéticas - ou do modo quântico - constituída por fótons. Se se quer determinar a posição do elétron, é necessário que a radiação tenha comprimento de onda da ordem da incerteza com que se quer determinar a posição.
Neste caso, quanto menor for o comprimento de onda (maior freqüência) maior é a precisão. Contudo, maior será a energia cedida pela radiação (onda ou fóton) em virtude da relação de Planck entre energia e freqüência da radiação
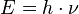
e o elétron sofrerá um recuo tanto maior quanto maior for essa energia, em virtude do efeito Compton. Como conseqüência, a velocidade sofrerá uma alteração não de todo previsível, ao contrário do que afirmaria a mecânica clássica.
Argumentos análogos poderiam ser usados para se demonstrar que ao se medir a velocidade com precisão, alterar-se-ia a posição de modo não totalmente previsível.
Resumidamente, pode-se dizer que tudo se passa de forma que quanto mais precisamente se medir uma grandeza, forçosamente mais será imprecisa a medida da grandeza correspondente, chamada decanonicamente conjugada
Algumas pessoas consideram mais fácil o entendimento através da analogia. Para se descobrir a posição de uma bola de plástico dentro de um quarto escuro, podemos emitir algum tipo de radiação e deduzir a posição da bola através das ondas que "batem" na bola e voltam. Se quisermos calcular a velocidade de um automóvel, podemos fazer com que ele atravesse dois feixes de luz, e calcular o tempo que ele levou entre um feixe e outro. Nem radiação nem a luz conseguem interferir de modo significativo na posição da bola, nem alterar a velocidade do automóvel. Mas podem interferir muito tanto na posição quanto na velocidade de um elétron, pois aí a diferença de tamanho entre o fóton de luz e o elétron é pequena. Seria, mais ou menos, como fazer o automóvel ter de atravessar dois troncos deárvores (o que certamente alteraria sua velocidade), ou jogar água dentro do quarto escuro, para deduzir a localização da bola através das pequenas ondas que baterão no objeto e voltarão; mas a água pode empurrar a bola mais para a frente, alterando sua posição. Desta forma torna-se impossivel determinar a localização real desta bola pois a própria determinação mudará a sua posição. Apesar disto, a sua nova posição pode ser ainda deduzida, calculando o quanto a bola seria empurrada sabendo a força das ondas obtendo-se uma posição provável da bola e sendo provável que a bola esteja localizada dentro daquela área.
Natureza da medida em mecânica quântica
Como se pode depreender da argumentação acima exposta, a natureza de uma medida sofre sérias reformulações no contexto da mecânica quântica. De fato, na mecânica quântica uma propriedade leva o nome de observável, pois não existem propriedades inobserváveis nesse contexto. Para a determinação de um observável, é necessário que se tenha uma preparação conveniente do aparato de medida, a fim de que se possa obter uma coleção de valores do ensemble de entes do sistema. Se não puder montar, ao menos teoricamente (em um Gedankenexperiment) uma preparação que possa medir tal grandeza (observável), então é impossível determiná-la naquelas condições do experimento.
Uma comparação tornará mais clara essa noção. No experimento de difração da dupla fenda, um feixe de elétrons atravessando uma fenda colimadora atinge mais adiante duas outras fendas paralelas traçadas numa parede opaca.
Do lado oposto da parede opaca, a luz, atravessando as fendas simultaneamente, atinge um anteparo. Se se puser sobre este um filme fotográfico, obtém-se pela revelação do filme um padrão de interferência de zonas claras e escuras. Esse resultado indica uma natureza ondulatória dos elétrons, resultado esse que motivou o desenvolvimento da mecânica quântica.
Entretanto, pode-se objetar e afirmar-se que a natureza dos elétrons seja corpuscular, ou seja, composta de fótons. Pode-se então perguntar por qual fenda o elétron atravessou para alcançar o anteparo. Para determinar isso, pode-se pôr, junto de cada fenda, uma pequena fonte luminosa que, ao menos em princípio, pode indicar a passagem dos elétrons por tal ou qual fenda. Entretanto, ao fazê-lo, o resultado do experimento é radicalmente mudado. A figura de interferência, antes presente, agora dá lugar a uma distribuição gaussiana bimodal de somente duas zonas claras em meio a uma zona escura, e cujos máximos se situam em frente às fendas.
Isso acontece porque as naturezas ondulatória e corpuscular do elétron não podem ser simultaneamente determinadas. A tentativa de determinar uma inviabiliza a determinação da outra. Essa constatação da dupla natureza da matéria (e da luz) leva o nome de princípio da complementaridade.
Essa analogia serve para mostrar como o mundo microfísico tem aspectos que diferem significativamente do que indica o senso comum.
Para se entender perfeitamente o alcance e o real significado do princípio da incerteza, é necessário que se distingam três tipos reconhecidos de propriedades dinâmicas em mecânica quântica:
- Propriedades compatíveis: são aquelas para as quais a medida simultânea e arbitrariamente precisa de seus valores não sofre nenhum tipo de restrição básica. Exemplo: a medição simultânea das coordenadas x, y e z de uma partícula. A medição simultânea dos momentos px,py e pz de uma partícula.
- Propriedades mutuamente excludentes: são aquelas para as quais a medida simultânea é simplesmente impossível. Exemplo: se um elétron está numa posição xi, não pode estar simultaneamente na posição diferente xj.
- Propriedades incompatíveis: são aquelas correspondentes a grandezas canonicamente conjugadas, ou seja, aquelas cujas medidas não podem ser simultaneamente medidas com precisão arbitrária. Em outras palavras, são grandezas cujas medidas simultâneas não podem ser levadas a cabo em um conjunto de subsistemas identicamente preparados (ensemble) para este fim, porque tal preparo não pode ser realizado. Exemplos: as coordenadas x,y e z e seus correspondentes momentos px,py e pz, respectivamente. As coordenadas angulares θi e os correspondentes momentos angulares Ji.
Observáveis e operadores
No formalismo matemático da mecânica quântica, os observáveis são representados por operadores matemáticos sobre um espaço de Hilbert.
Esses operadores podem ser construídos a partir de seus equivalentes clássicos.
Na formulação de Heisenberg, as relações da incerteza podem ser dados na forma de um operador comutador, que opera sobre dois outros operadores quaisquer:
![[A,B] \equiv AB - BA](http://upload.wikimedia.org/math/8/7/c/87c57d02df8655e838ab1f5cb596f66a.png)
onde A e B são operadores quaisquer.
No caso das relações de incerteza:
![[X_k,B_l] = i\hbar\delta_{kl}\mathbb{I}](http://upload.wikimedia.org/math/a/5/1/a5159c7789b1e88c2cf549a63309de44.png)
Dirac notou a semelhança formal entre o comutador e os parênteses de Poisson. Sabedor da equivalência usada por Schrödinger quando este postulou a forma da equação de onda, Dirac postulou as seguintes equivalências, que valem como receita para se acharem os operadores quânticos correspondentes a grandezas clássicas:


![\left \{x_k,p_l\right\}\to \frac{1}{i\ \hbar}\cdot \left[X_k,P_l\right]](http://upload.wikimedia.org/math/4/7/c/47cf3f71be3cbd626dc4fc450b736ac2.png)
A descrição ondulatória dos objetos microscópicos tem consequências teóricas importantes, como o principio da incerteza de Heisenberg. O fato de os objetos microscópicos, em muitas situações, terem uma localização no espaço mesmo que aproximada, implica que não podem ser descritos por uma onda com um só comprimento de onda (onda plana), pois esta ocuparia todo o espaço. É necessária uma superposição de comprimentos de ondas diferentes para se obter um "pacote" de ondas mais bem localizado e que represente o objeto microscópico.
O papel do princípio da incerteza nas formulações modernas da mecânica quântica
Hoje em dia, o princípio da incerteza é importante principalmente por dois motivos: um histórico e outro didático. Ambos são análogos: o princípio da incerteza mostra de maneira clara que concepções clássicas a respeito da medida devem ser abandonadas.
No entanto, o princípio da incerteza *não* é um bom princípio (ou postulado) da mecânica quântica, já que é inexato e pouco geral. A mecânica quântica não-relativística é totalmente descrita com alguns postulados, dos quais as relações de incerteza de Heisenberg surgem de forma pouco natural. Mas o espírito do princípio da incerteza é mantido: não se pode ter um sistema que, ao ser medido, tenha a probabilidade 1 de se encontrar tanto uma ou outra grandeza, se essas grandezas corresponderem a operadores que não comutam. Iremos explicar isto melhor adiante:
Todas as grandezas que podem ser medidas correspondem aos chamados "autovalores" de certos objetos matemáticos chamados de operadores (na verdade, a natureza requer que esses operadores sejam de uma classe especial, a dos "observáveis"). Chamemos um operador qualquer de A, e chamemos seus autovalores de a_n (a_1 é um autovalor, a_2 é outro e assim por diante). Existem estados quânticos, chamados "autoestados" (que representaremos por  ) do operador A, nos quais uma medida tem 100% de chance de encontrar o valor a_n. Esses autoestados e esses autovalores são definidos pela seguinte equação:
) do operador A, nos quais uma medida tem 100% de chance de encontrar o valor a_n. Esses autoestados e esses autovalores são definidos pela seguinte equação:
 ) do operador A, nos quais uma medida tem 100% de chance de encontrar o valor a_n. Esses autoestados e esses autovalores são definidos pela seguinte equação:
) do operador A, nos quais uma medida tem 100% de chance de encontrar o valor a_n. Esses autoestados e esses autovalores são definidos pela seguinte equação:
Um operador é dito um observável se esses autoestados  formarem uma "base". Diz-se que um grupo qualquer de estados quânticos formam uma base se qualquer outro estado quântico puder ser escrito como uma superposição deles. Ou seja, para qualquer estado quântico
formarem uma "base". Diz-se que um grupo qualquer de estados quânticos formam uma base se qualquer outro estado quântico puder ser escrito como uma superposição deles. Ou seja, para qualquer estado quântico  ,
,
 formarem uma "base". Diz-se que um grupo qualquer de estados quânticos formam uma base se qualquer outro estado quântico puder ser escrito como uma superposição deles. Ou seja, para qualquer estado quântico
formarem uma "base". Diz-se que um grupo qualquer de estados quânticos formam uma base se qualquer outro estado quântico puder ser escrito como uma superposição deles. Ou seja, para qualquer estado quântico  ,
,
Onde os coeficientes  , em geral complexos, indicam o quanto os autoestados correspondentes
, em geral complexos, indicam o quanto os autoestados correspondentes  influenciam no estado resultante,
influenciam no estado resultante,  . Um dos postulados da mecânica quântica diz que a probabilidade de uma medida da grandeza A revelar o valor a_n é:
. Um dos postulados da mecânica quântica diz que a probabilidade de uma medida da grandeza A revelar o valor a_n é:
 , em geral complexos, indicam o quanto os autoestados correspondentes
, em geral complexos, indicam o quanto os autoestados correspondentes  influenciam no estado resultante,
influenciam no estado resultante,  . Um dos postulados da mecânica quântica diz que a probabilidade de uma medida da grandeza A revelar o valor a_n é:
. Um dos postulados da mecânica quântica diz que a probabilidade de uma medida da grandeza A revelar o valor a_n é: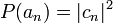
Quando o sistema está no autoestado  , o postulado acima mostra que a probabilidade de se encontrar o valor a_n correspondente é 100%. Assim, pode-se dizer que o sistema *possui a grandeza A bem definida*.
, o postulado acima mostra que a probabilidade de se encontrar o valor a_n correspondente é 100%. Assim, pode-se dizer que o sistema *possui a grandeza A bem definida*.
 , o postulado acima mostra que a probabilidade de se encontrar o valor a_n correspondente é 100%. Assim, pode-se dizer que o sistema *possui a grandeza A bem definida*.
, o postulado acima mostra que a probabilidade de se encontrar o valor a_n correspondente é 100%. Assim, pode-se dizer que o sistema *possui a grandeza A bem definida*.
Agora consideremos dois operadores A e B, como o operador da posição e o operador do momento. Em geral, os autoestados de um operador não são os mesmos autoestados do outro operador. Consequentemente, se o sistema está em um estado quântico onde a grandeza A é bem definida, a grandeza B não será bem definida. Ou seja, haverá uma "incerteza" na grandeza B.
Mas, e se o sistema estiver num estado onde a grandeza A é bem definida, e efetuarmos uma medida na grandeza B? Pode-se pensar que, então, saberemos exatamente o valor de ambas as grandezas. Mas isso está errado, devido a outro dos postulados da mecânica quântica: se uma medida de uma grandeza qualquer B revela o valor b_n, então o sistema *é perturbado pela medida*, e passa para o autoestado  correspondente à grandeza B_n.
correspondente à grandeza B_n.
 correspondente à grandeza B_n.
correspondente à grandeza B_n.
Então, suponha que dois operadores A e B não possuem os mesmos autoestados. Se efetuarmos em um sistema qualquer a medida da grandeza A, e encontrarmos um certo valor, o sistema se torna um autoestado de A, com um valor bem definido de A e uma incerteza no valor de B. Se, após isso, efetuarmos uma medida no valor de B, então lançamos o sistema num autoestado de B, com um valor bem definido de B e uma incerteza no valor de A. Com isso, dizemos que é impossível saber simultaneamente o valor da grandeza A e da grandeza B.
A incerteza entre a posição e o momento proposta por Heisenberg é, então, uma consequência dos postulados da mecânica quântica, e não um postulado por si só.
Fonte: wikipedia é a
é a
Nenhum comentário:
Postar um comentário